Loading...
Searching...
No Matches
tensor::triple_tensor_product Interface Reference
Public Member Functions | |
| subroutine | triple_tensor_product_scalar (v, u, nu, hr, hs, ht) |
| Computes the tensor product \( v =(H_t \otimes H_s \otimes H_r) u \). This operation is usually performed for spectral interpolation of a scalar field as defined by. | |
| subroutine | triple_tensor_product_vector (v, u1, u2, u3, nu, hr, hs, ht) |
| Computes the tensor product on a vector field \( \mathbf{v} =(H_t \otimes H_s \otimes H_r) \mathbf{u} \). This operation is usually performed for spectral interpolation on a 3D vector field \( \mathbf{u} = (u_1,u_2,u_3) \) as defined by. | |
Detailed Description
Definition at line 81 of file tensor.f90.
Member Function/Subroutine Documentation
◆ triple_tensor_product_scalar()
| subroutine tensor::triple_tensor_product::triple_tensor_product_scalar | ( | real(kind=rp), intent(inout) | v, |
| real(kind=rp), dimension(nu, nu, nu), intent(inout) | u, | ||
| integer, intent(in) | nu, | ||
| real(kind=rp), dimension(nu), intent(inout) | hr, | ||
| real(kind=rp), dimension(nu), intent(inout) | hs, | ||
| real(kind=rp), dimension(nu), intent(inout) | ht | ||
| ) |
\begin{eqnarray*} v(r,s,t) = \sum_{i=0}^{N}{\sum_{j=0}^{N}{ \sum_{k=0}^{N}{u_{ijk}h_i(r)h_j(s)h_k(t)}}} \end{eqnarray*}
- Parameters
-
v Interpolated value (scalar). u Field values at the GLL points (e.g. velocity in x-direction). nu Size of the interpolation weights (usually lx).Hr Interpolation weights in the r-direction. Hs Interpolation weights in the s-direction. Ht Interpolation weights in the t-direction.
Definition at line 312 of file tensor.f90.
Here is the call graph for this function:
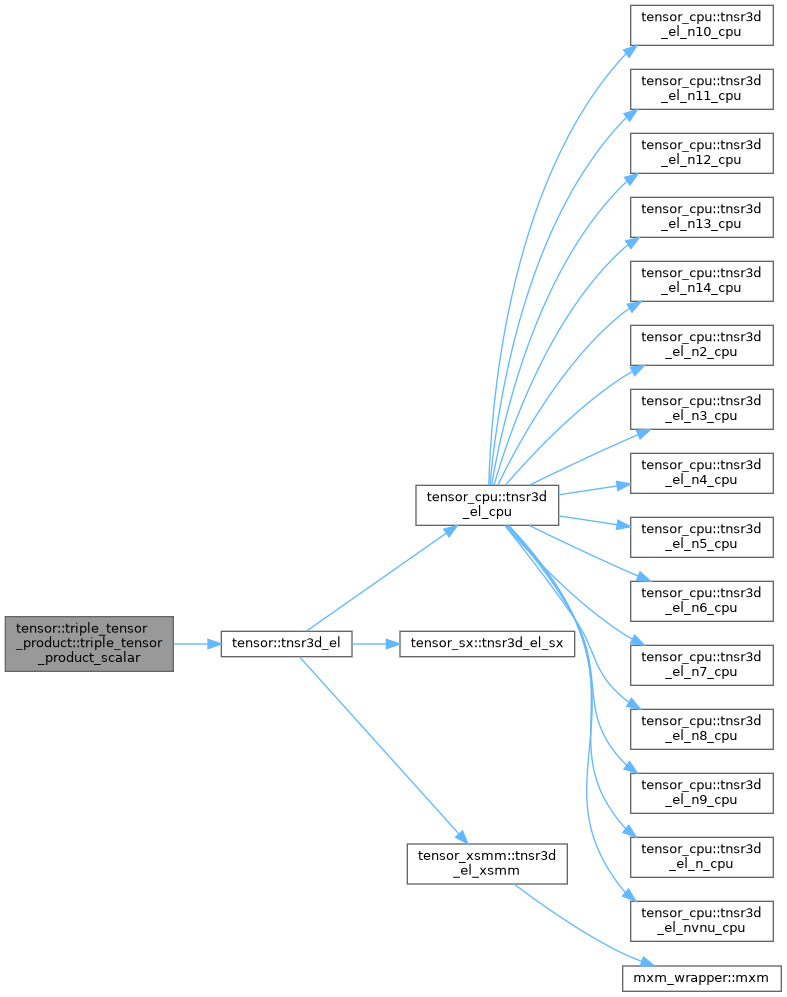
◆ triple_tensor_product_vector()
| subroutine tensor::triple_tensor_product::triple_tensor_product_vector | ( | real(kind=rp), dimension(3), intent(inout) | v, |
| real(kind=rp), dimension(nu, nu, nu), intent(inout) | u1, | ||
| real(kind=rp), dimension(nu, nu, nu), intent(inout) | u2, | ||
| real(kind=rp), dimension(nu, nu, nu), intent(inout) | u3, | ||
| integer, intent(in) | nu, | ||
| real(kind=rp), dimension(nu), intent(inout) | hr, | ||
| real(kind=rp), dimension(nu), intent(inout) | hs, | ||
| real(kind=rp), dimension(nu), intent(inout) | ht | ||
| ) |
\begin{eqnarray*} \mathbf{v}(r,s,t) = \sum_{i=0}^{N}{\sum_{j=0}^{N}{ \sum_{k=0}^{N}{\mathbf{u}_{ijk}h_i(r)h_j(s)h_k(t)}}} \end{eqnarray*}
- Parameters
-
v Interpolated value (scalar). u1 3D-array containing values at the GLL points (e.g. velocity). u2 3D-array containing values at the GLL points (e.g. velocity). u3 3D-array containing values at the GLL points (e.g. velocity). nu Size of the interpolation weights (usually lx).Hr Interpolation weights in the r-direction. Hs Interpolation weights in the s-direction. Ht Interpolation weights in the t-direction.
Definition at line 348 of file tensor.f90.
Here is the call graph for this function:

The documentation for this interface was generated from the following file:
- /home/runner/work/neko/neko/src/math/tensor.f90