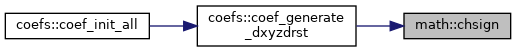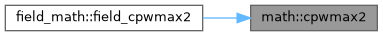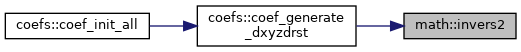|
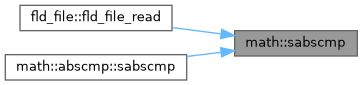
| pure logical function, public | sabscmp (x, y, tol) |
| | Return single precision absolute comparison \( | x - y | < \epsilon \).
|
| |
| pure logical function, public | dabscmp (x, y, tol) |
| | Return double precision absolute comparison \( | x - y | < \epsilon \).
|
| |
| pure logical function | qabscmp (x, y, tol) |
| | Return double precision absolute comparison \( | x - y | < \epsilon \).
|
| |
| pure logical function | srelcmp (x, y, eps) |
| | Return single precision relative comparison \( | x - y |<= \epsilon*|y| \).
|
| |
| pure logical function | drelcmp (x, y, eps) |
| | Return double precision relative comparison \( | x - y |/|y| < \epsilon \).
|
| |
| pure logical function | qrelcmp (x, y, eps) |
| | Return quad precision relative comparison \( | x - y |/|y| < \epsilon \).
|
| |
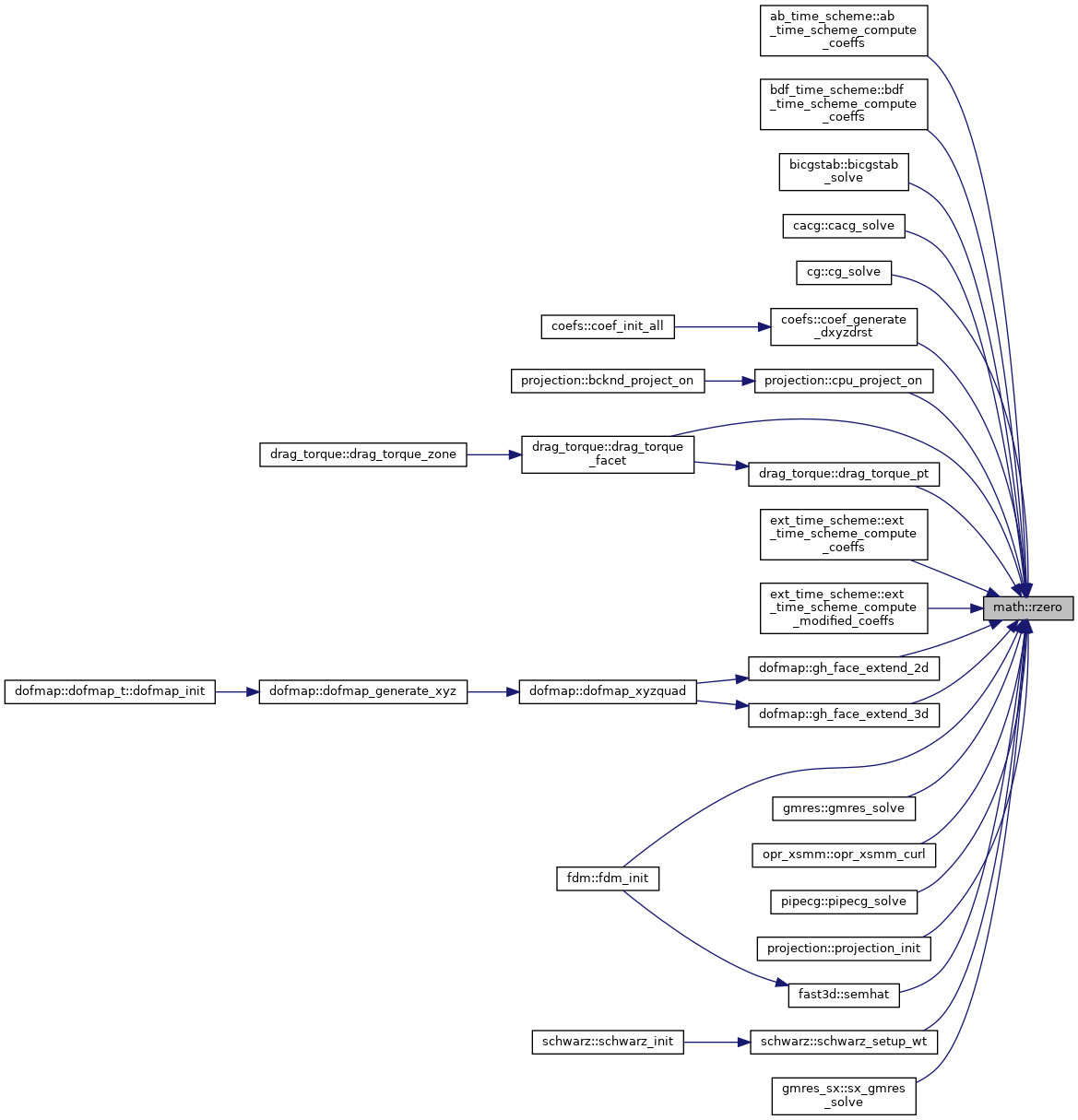
| subroutine, public | rzero (a, n) |
| | Zero a real vector.
|
| |
| subroutine, public | izero (a, n) |
| | Zero an integer vector.
|
| |
| subroutine, public | row_zero (a, m, n, e) |
| | Sets row e to 0 in matrix a.
|
| |
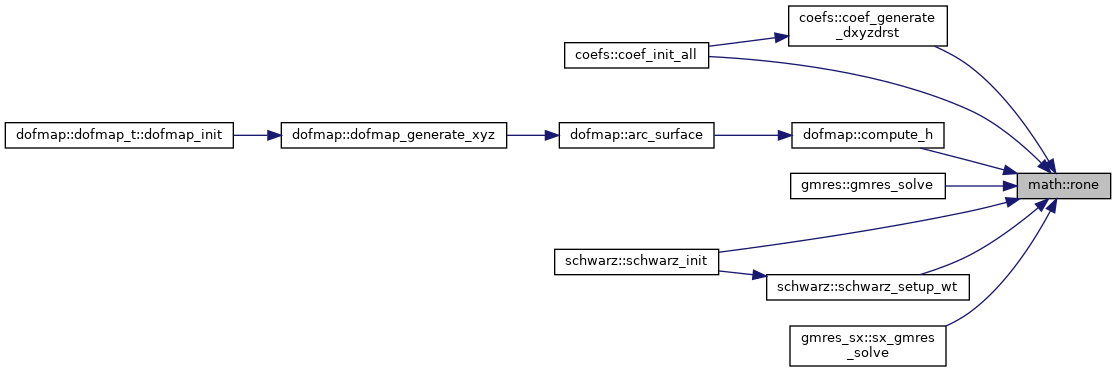
| subroutine, public | rone (a, n) |
| | Set all elements to one.
|
| |
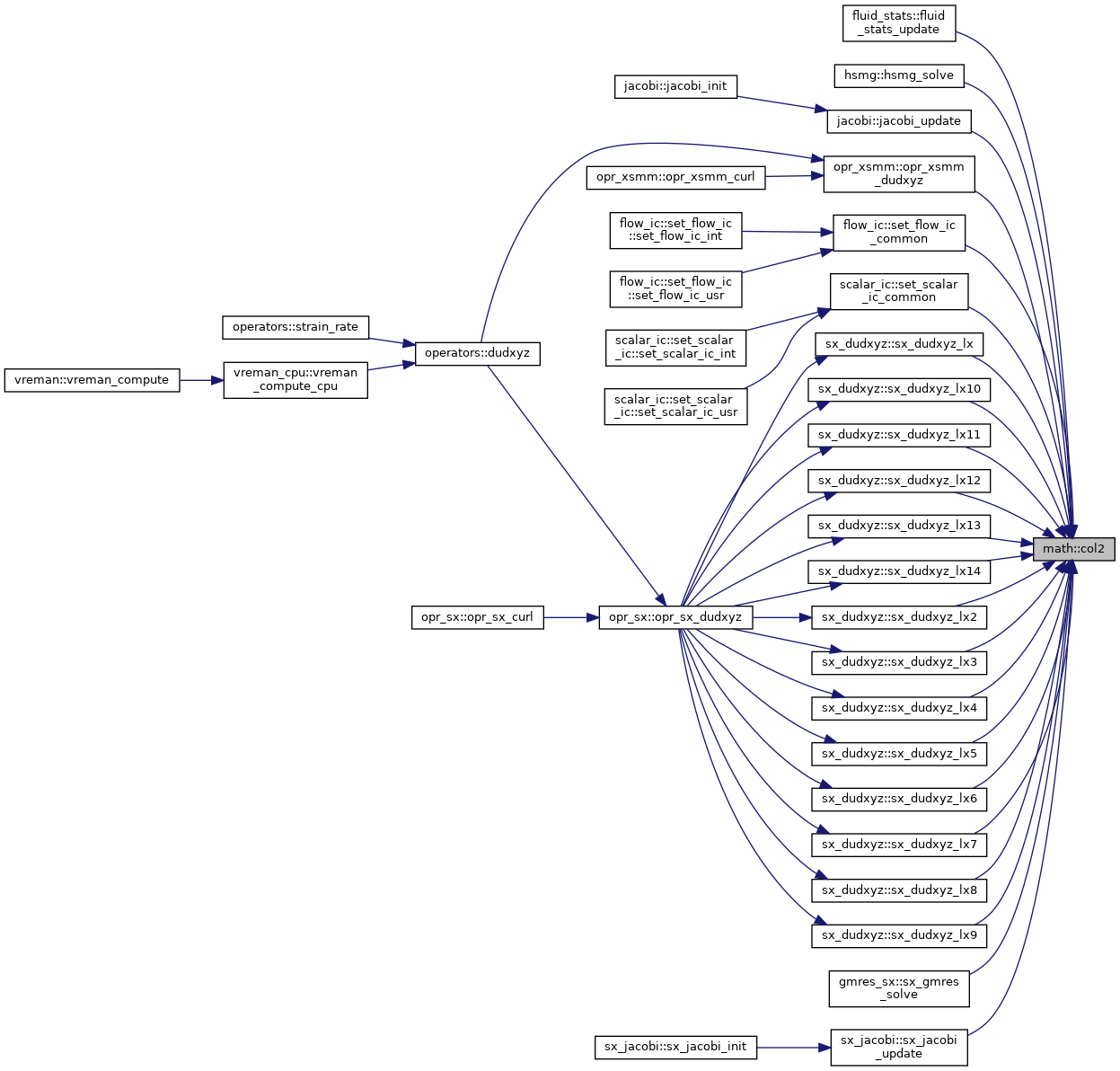
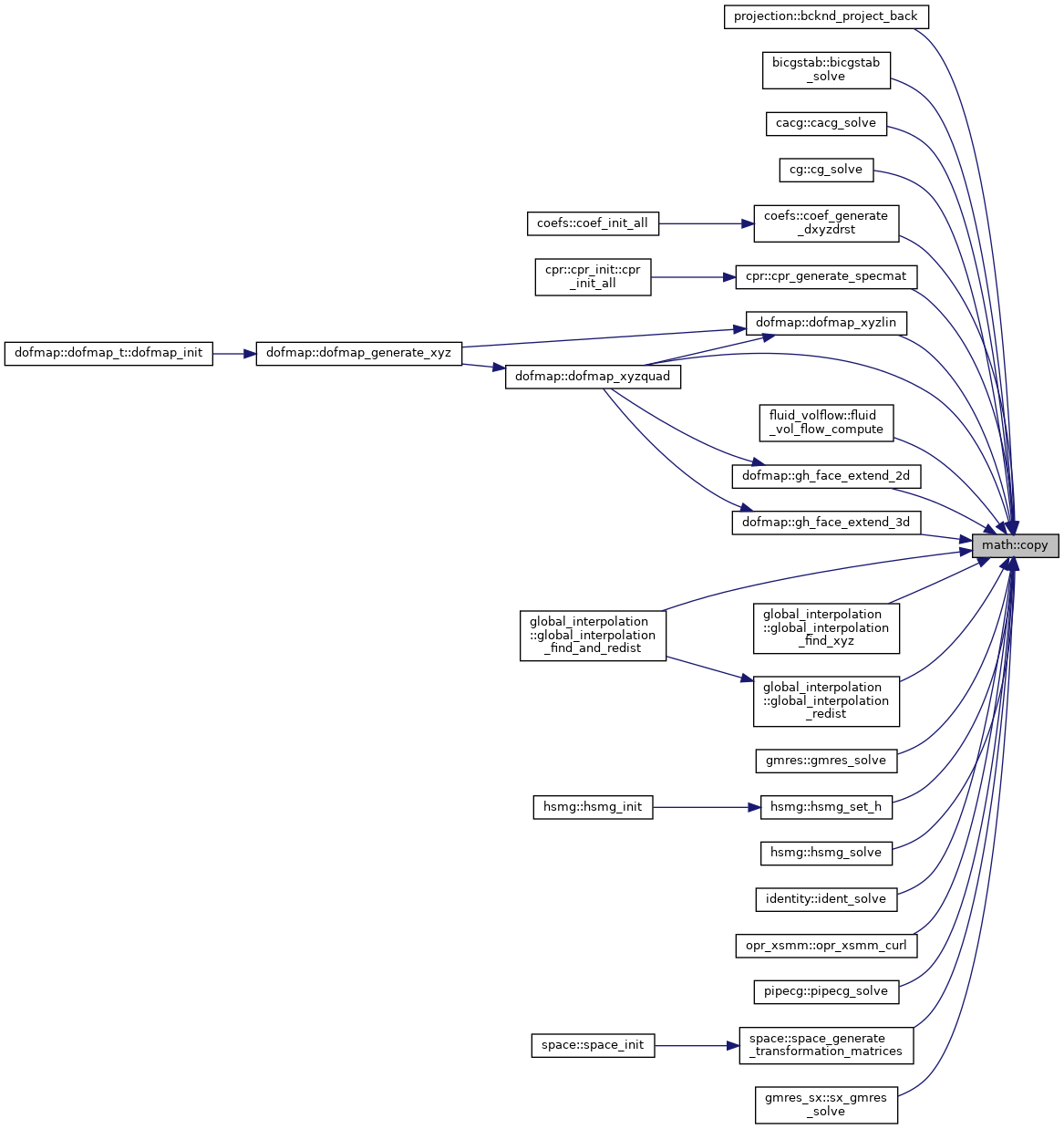
| subroutine, public | copy (a, b, n) |
| | Copy a vector \( a = b \).
|
| |
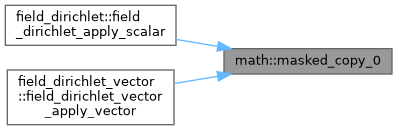
| subroutine, public | masked_copy_0 (a, b, mask, n, n_mask) |
| | Copy a masked vector \( a(mask) = b(mask) \).
|
| |
| subroutine, public | masked_copy (a, b, mask, n, n_mask) |
| | Copy a masked vector \( a(mask) = b(mask) \).
|
| |
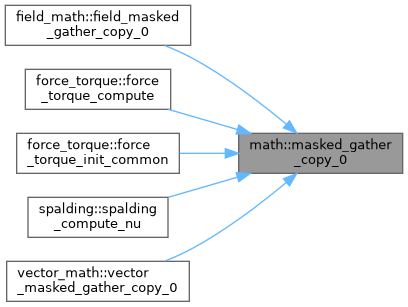
| subroutine, public | masked_gather_copy_0 (a, b, mask, n, n_mask) |
| | Gather a masked vector to reduced contigous vector \( a = b(mask) \).
|
| |
| subroutine, public | masked_gather_copy (a, b, mask, n, n_mask) |
| | Gather a masked vector to reduced contigous vector \( a = b(mask) \).
|
| |
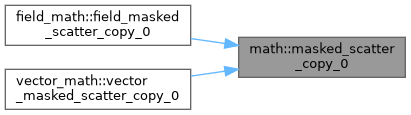
| subroutine, public | masked_scatter_copy_0 (a, b, mask, n, n_mask) |
| | Scatter a contigous vector to masked positions in a target array \( a(mask) = b \).
|
| |
| subroutine, public | masked_scatter_copy (a, b, mask, n, n_mask) |
| | Scatter a contigous vector to masked positions in a target array \( a(mask) = b \).
|
| |
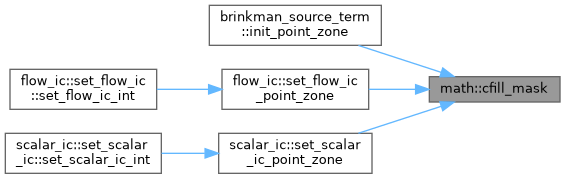
| subroutine, public | cfill_mask (a, c, n, mask, n_mask) |
| | Fill a constant to a masked vector. \( a_i = c, for i in mask \).
|
| |
| subroutine, public | cmult (a, c, n) |
| | Multiplication by constant c \( a = c \cdot a \).
|
| |
| subroutine, public | cmult2 (a, b, c, n) |
| | Multiplication by constant c \( a = c \cdot b \).
|
| |
| subroutine, public | cdiv (a, c, n) |
| | Division of constant c by elements of a \( a = c / a \).
|
| |
| subroutine, public | cdiv2 (a, b, c, n) |
| | Division of constant c by elements of a \( a = c / b \).
|
| |
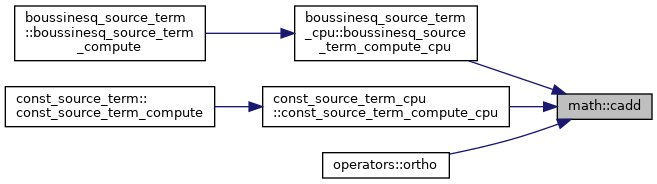
| subroutine, public | cadd (a, s, n) |
| | Add a scalar to vector \( a_i = a_i + s \).
|
| |
| subroutine, public | cadd2 (a, b, s, n) |
| | Add a scalar to vector \( a_i = b_i + s \).
|
| |
| subroutine, public | cfill (a, c, n) |
| | Set all elements to a constant c \( a = c \).
|
| |
| real(kind=rp) function, public | glsum (a, n) |
| | Sum a vector of length n.
|
| |
| real(kind=rp) function, public | glmax (a, n) |
| | Max of a vector of length n.
|
| |
| integer function, public | glimax (a, n) |
| | Max of an integer vector of length n.
|
| |
| real(kind=rp) function, public | glmin (a, n) |
| | Min of a vector of length n.
|
| |
| integer function, public | glimin (a, n) |
| | Min of an integer vector of length n.
|
| |
| subroutine, public | chsign (a, n) |
| | Change sign of vector \( a = -a \).
|
| |
| real(kind=rp) function, public | vlmax (vec, n) |
| | maximum value of a vector of length n
|
| |
| real(kind=rp) function, public | vlmin (vec, n) |
| | minimun value of a vector of length n
|
| |
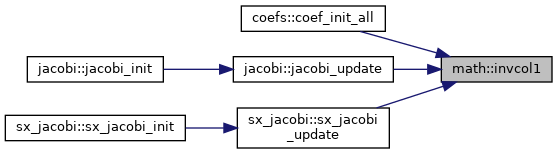
| subroutine, public | invcol1 (a, n) |
| | Invert a vector \( a = 1 / a \).
|
| |
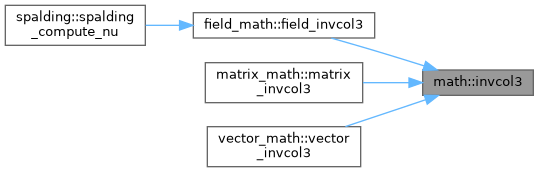
| subroutine, public | invcol3 (a, b, c, n) |
| | Invert a vector \( a = b / c \).
|
| |
| subroutine, public | invers2 (a, b, n) |
| | Compute inverted vector \( a = 1 / b \).
|
| |
| subroutine, public | vcross (u1, u2, u3, v1, v2, v3, w1, w2, w3, n) |
| | Compute a cross product \( u = v \times w \) assuming vector components \( u = (u_1, u_2, u_3) \) etc.
|
| |
| subroutine, public | vdot2 (dot, u1, u2, v1, v2, n) |
| | Compute a dot product \( dot = u \cdot v \) (2-d version) assuming vector components \( u = (u_1, u_2, u_3) \) etc.
|
| |
| subroutine, public | vdot3 (dot, u1, u2, u3, v1, v2, v3, n) |
| | Compute a dot product \( dot = u \cdot v \) (3-d version) assuming vector components \( u = (u_1, u_2, u_3) \) etc.
|
| |
| real(kind=rp) function, public | vlsc3 (u, v, w, n) |
| | Compute multiplication sum \( dot = u \cdot v \cdot w \).
|
| |
| real(kind=rp) function, public | vlsc2 (u, v, n) |
| | Compute multiplication sum \( dot = u \cdot v \cdot w \).
|
| |
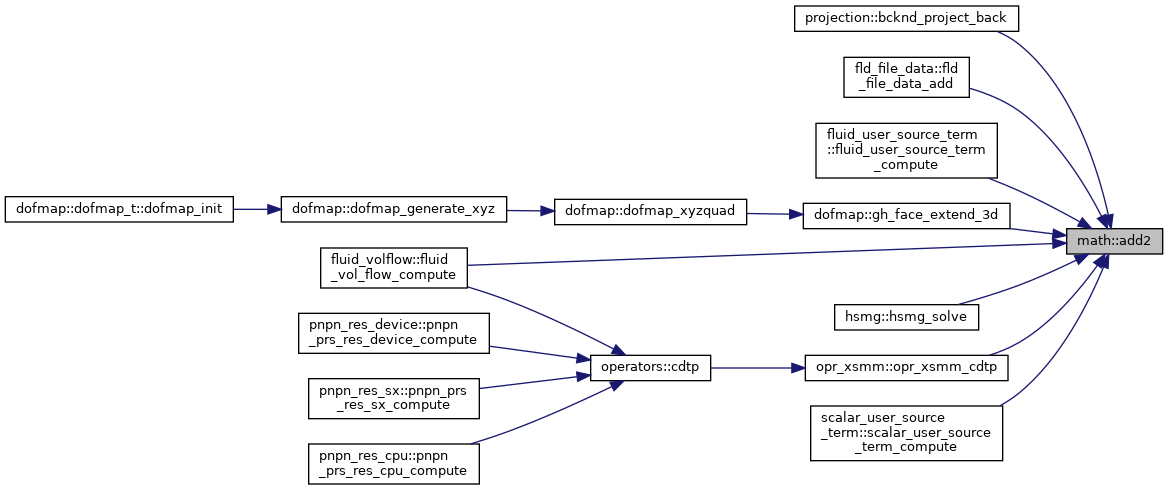
| subroutine, public | add2 (a, b, n) |
| | Vector addition \( a = a + b \).
|
| |
| subroutine, public | add3 (a, b, c, n) |
| | Vector addition \( a = b + c \).
|
| |
| subroutine, public | add4 (a, b, c, d, n) |
| | Vector addition \( a = b + c + d\).
|
| |
| subroutine, public | sub2 (a, b, n) |
| | Vector substraction \( a = a - b \).
|
| |
| subroutine, public | sub3 (a, b, c, n) |
| | Vector subtraction \( a = b - c \).
|
| |
| subroutine, public | add2s1 (a, b, c1, n) |
| | Vector addition with scalar multiplication \( a = c_1 a + b \) (multiplication on first argument)
|
| |
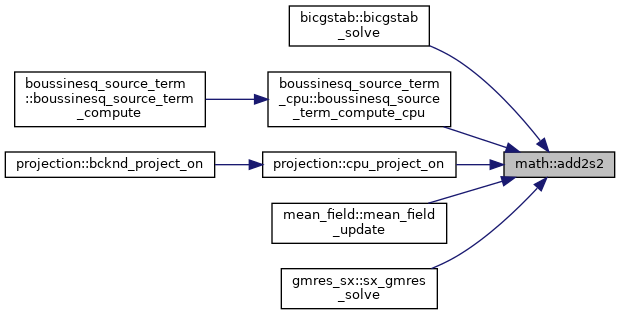
| subroutine, public | add2s2 (a, b, c1, n) |
| | Vector addition with scalar multiplication \( a = a + c_1 b \) (multiplication on second argument)
|
| |
| subroutine, public | addsqr2s2 (a, b, c1, n) |
| | Returns \( a = a + c1 * (b * b )\).
|
| |
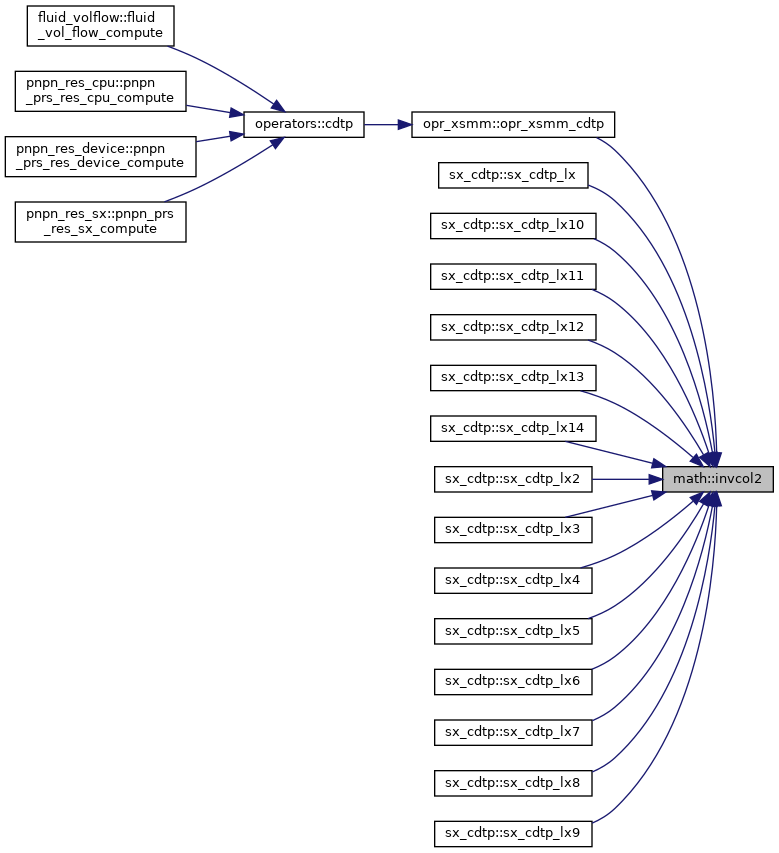
| subroutine, public | invcol2 (a, b, n) |
| | Vector division \( a = a / b \).
|
| |
| subroutine, public | col2 (a, b, n) |
| | Vector multiplication \( a = a \cdot b \).
|
| |
| subroutine, public | col3 (a, b, c, n) |
| | Vector multiplication with 3 vectors \( a = b \cdot c \).
|
| |
| subroutine, public | subcol3 (a, b, c, n) |
| | Returns \( a = a - b*c \).
|
| |
| subroutine, public | add3s2 (a, b, c, c1, c2, n) |
| | Returns \( a = c1 * b + c2 * c \).
|
| |
| subroutine, public | add4s3 (a, b, c, d, c1, c2, c3, n) |
| | Returns \( a = c1 * b + c2 * c + c3 * d \).
|
| |
| subroutine, public | add5s4 (a, b, c, d, e, c1, c2, c3, c4, n) |
| | Returns \( a = a + c1 * b + c2 * c + c3 * d + c4 * e\).
|
| |
| subroutine, public | subcol4 (a, b, c, d, n) |
| | Returns \( a = a - b*c*d \).
|
| |
| subroutine, public | addcol3 (a, b, c, n) |
| | Returns \( a = a + b*c \).
|
| |
| subroutine, public | addcol4 (a, b, c, d, n) |
| | Returns \( a = a + b*c*d \).
|
| |
| subroutine, public | addcol3s2 (a, b, c, s, n) |
| | Returns \( a = a + s(b*c) \).
|
| |
| subroutine, public | ascol5 (a, b, c, d, e, n) |
| | Returns \( a = b \dot c - d \cdot e \).
|
| |
| subroutine, public | p_update (a, b, c, c1, c2, n) |
| | Returns \( a = b \dot c1 ( a - c2 \cdot c )\).
|
| |
| subroutine, public | x_update (a, b, c, c1, c2, n) |
| | Returns \( a = b \dot c1 ( a - c2 \cdot c )\).
|
| |
| real(kind=rp) function, public | glsc2 (a, b, n) |
| | Weighted inner product \( a^T b \).
|
| |
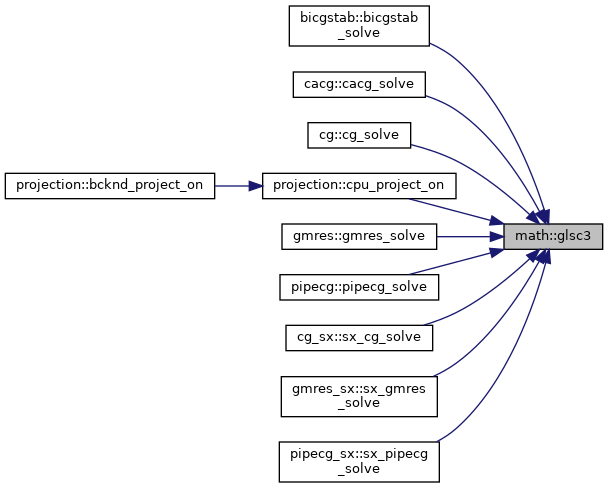
| real(kind=rp) function, public | glsc3 (a, b, c, n) |
| | Weighted inner product \( a^T b c \).
|
| |
| real(kind=rp) function, public | glsc4 (a, b, c, d, n) |
| |
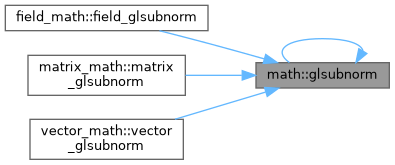
| real(kind=rp) function, public | glsubnorm (a, b, n) |
| | Returns the norm of the difference of two vectors \( \sqrt{(a-b)^T (a-b)} \).
|
| |
| subroutine | sortrp (a, ind, n) |
| | Heap Sort for double precision arrays.
|
| |
| subroutine | sorti4 (a, ind, n) |
| | Heap Sort for single integer arrays.
|
| |
| subroutine | swapdp (b, ind, n) |
| | sort double precision array acording to ind vector
|
| |
| subroutine | swapi4 (b, ind, n) |
| | sort single integer array acording to ind vector
|
| |
| subroutine | reorddp (b, ind, n) |
| | reorder double precision array - inverse of swap
|
| |
| subroutine | reordi4 (b, ind, n) |
| | reorder single integer array - inverse of swap
|
| |
| subroutine | flipvdp (b, ind, n) |
| | Flip double precision vector b and ind.
|
| |
| subroutine | flipvi4 (b, ind, n) |
| | Flip single integer vector b and ind.
|
| |
| subroutine, public | absval (a, n) |
| | Take the absolute value of an array.
|
| |
| subroutine, public | pwmax2 (a, b, n) |
| | Point-wise maximum of two vectors \( a = \max(a, b) \).
|
| |
| subroutine, public | pwmax3 (a, b, c, n) |
| | Point-wise maximum of two vectors \( a = \max(b, c) \).
|
| |
| subroutine, public | cpwmax2 (a, b, n) |
| | Point-wise maximum of scalar and vector \( a = \max(a, b) \).
|
| |
| subroutine, public | cpwmax3 (a, b, c, n) |
| | Point-wise maximum of scalar and vector \( a = \max(b, c) \).
|
| |
| subroutine, public | pwmin2 (a, b, n) |
| | Point-wise minimum of two vectors \( a = \min(a, b) \).
|
| |
| subroutine, public | pwmin3 (a, b, c, n) |
| | Point-wise minimum of two vectors \( a = \min(b, c) \).
|
| |
| subroutine, public | cpwmin2 (a, b, n) |
| | Point-wise minimum of scalar and vector \( a = \min(a, b) \).
|
| |
| subroutine, public | cpwmin3 (a, b, c, n) |
| | Point-wise minimum of scalar and vector \( a = \min(b, c) \).
|
| |
| real(rp) function, dimension(3, 3), public | matinv39 (a11, a12, a13, a21, a22, a23, a31, a32, a33) |
| |
| real(kind=xp) function, dimension(3, 3), public | matinv3 (a) |
| | Performs a direct calculation of the inverse of a 3×3 matrix. M33INV and M44INV by David G. Simpson pure function version from https://fortranwiki.org/fortran/show/Matrix+inversion Invert 3x3 matrix.
|
| |