Functions/Subroutines
subroutine, public	field_rzero (a, n)
	Zero a real vector.

subroutine, public	field_rone (a, n)
	Set all elements to one.

subroutine, public	field_copy (a, b, n)
	Copy a vector \( a = b \).

subroutine, public	field_cmult (a, c, n)
	Multiplication by constant c \( a = c \cdot a \).

subroutine, public	field_cadd (a, s, n)
	Add a scalar to vector \( a = \sum a_i + s \).

subroutine, public	field_cfill (a, c, n)
	Set all elements to a constant c \( a = c \).

subroutine, public	field_invcol1 (a, n)
	Invert a vector \( a = 1 / a \).

subroutine, public	field_invcol3 (a, b, c, n)
	Invert a vector \( a = b / c \).

subroutine, public	field_vdot3 (dot, u1, u2, u3, v1, v2, v3, n)
	Compute a dot product \( dot = u \cdot v \) (3-d version) assuming vector components \( u = (u_1, u_2, u_3) \) etc.

subroutine, public	field_add2 (a, b, n)
	Vector addition \( a = a + b \).

subroutine, public	field_add3 (a, b, c, n)
	Vector addition \( a = b + c \).

subroutine	field_add4 (a, b, c, d, n)
	Vector addition \( a = b + c + d \).

subroutine, public	field_sub2 (a, b, n)
	Vector substraction \( a = a - b \).

subroutine, public	field_sub3 (a, b, c, n)
	Vector subtraction \( a = b - c \).

subroutine, public	field_add2s1 (a, b, c1, n)
	Vector addition with scalar multiplication \( a = c_1 a + b \) (multiplication on first argument)

subroutine, public	field_add2s2 (a, b, c1, n)
	Vector addition with scalar multiplication \( a = a + c_1 b \) (multiplication on second argument)

subroutine, public	field_addsqr2s2 (a, b, c1, n)
	Returns \( a = a + c1 * (b * b )\).

subroutine, public	field_cmult2 (a, b, c, n)
	Multiplication by constant c \( a = c \cdot b \).

subroutine, public	field_invcol2 (a, b, n)
	Vector division \( a = a / b \).

subroutine, public	field_col2 (a, b, n)
	Vector multiplication \( a = a \cdot b \).

subroutine, public	field_col3 (a, b, c, n)
	Vector multiplication with 3 vectors \( a = b \cdot c \).

subroutine, public	field_subcol3 (a, b, c, n)
	Returns \( a = a - b*c \).

subroutine, public	field_add3s2 (a, b, c, c1, c2, n)
	Returns \( a = c1 * b + c2 * c \).

subroutine, public	field_addcol3 (a, b, c, n)
	Returns \( a = a + b*c \).

subroutine, public	field_addcol4 (a, b, c, d, n)
	Returns \( a = a + bcd \).

real(kind=rp) function, public	field_glsum (a, n)

real(kind=rp) function, public	field_glsc2 (a, b, n)

real(kind=rp) function, public	field_glsc3 (a, b, c, n)

real(kind=rp) function, public	field_glsubnorm (a, b, n)

subroutine, public	field_masked_gather_copy_0 (a, b, mask, n, n_mask)
	Gather a field to reduced contigous array \( a = b(mask) \).

subroutine, public	field_masked_scatter_copy_0 (a, b, mask, n, n_mask)
	Gather a contigous array into a field \( a(mask) = b \).

subroutine, public	field_pwmax2 (a, b, n)
	Point-wise max operation \( a = max(a,b) \).

subroutine, public	field_pwmax3 (a, b, c, n)
	Point-wise max operation \( a = max(b, c) \).

subroutine, public	field_cpwmax2 (a, b, n)
	Point-wise max operation for field and constant \( a(i) = max(a(i), b) \).

subroutine, public	field_cpwmax3 (a, b, c, n)
	Point-wise max operation for field and constant \( a(i) = max(b(i), c) \).

subroutine, public	field_pwmin2 (a, b, n)
	Point-wise min operation \( a = min(a,b) \).

subroutine, public	field_pwmin3 (a, b, c, n)
	Point-wise min operation \( a = min(b, c) \).

subroutine, public	field_cpwmin2 (a, b, n)
	Point-wise min operation for field and constant \( a(i) = min(a(i), b) \).

subroutine, public	field_cpwmin3 (a, b, c, n)
	Point-wise min operation for field and constant \( a(i) = min(b(i), c) \).

Function/Subroutine Documentation

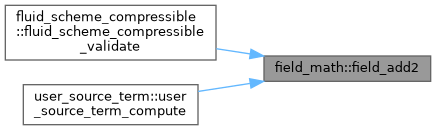
◆ field_add2()

subroutine, public field_math::field_add2	(	type(field_t), intent(inout)	a,
		type(field_t), intent(in)	b,
		integer, intent(in), optional	n
	)

Definition at line 287 of file field_math.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ field_add2s1()

subroutine, public field_math::field_add2s1	(	type(field_t), intent(inout)	a,
		type(field_t), intent(inout)	b,
		real(kind=rp), intent(in)	c1,
		integer, intent(in), optional	n
	)

Definition at line 395 of file field_math.f90.

Here is the call graph for this function:

◆ field_add2s2()

subroutine, public field_math::field_add2s2	(	type(field_t), intent(inout)	a,
		type(field_t), intent(inout)	b,
		real(kind=rp), intent(in)	c1,
		integer, intent(in), optional	n
	)

Definition at line 418 of file field_math.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

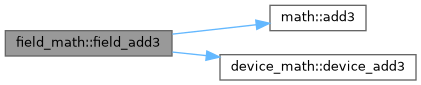
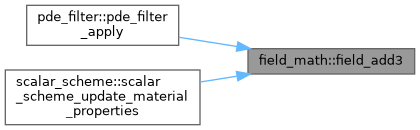
◆ field_add3()

subroutine, public field_math::field_add3	(	type(field_t), intent(inout)	a,
		type(field_t), intent(in)	b,
		type(field_t), intent(in)	c,
		integer, intent(in), optional	n
	)

Definition at line 308 of file field_math.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ field_add3s2()

subroutine, public field_math::field_add3s2	(	type(field_t), intent(inout)	a,
		type(field_t), intent(in)	b,
		type(field_t), intent(in)	c,
		real(kind=rp), intent(in)	c1,
		real(kind=rp), intent(in)	c2,
		integer, intent(in), optional	n
	)

Definition at line 571 of file field_math.f90.

Here is the call graph for this function:

◆ field_add4()

subroutine field_math::field_add4	(	type(field_t), intent(inout)	a,
		type(field_t), intent(in)	b,
		type(field_t), intent(in)	c,
		type(field_t), intent(in)	d,
		integer, intent(in), optional	n
	)

private

Definition at line 329 of file field_math.f90.

Here is the call graph for this function:

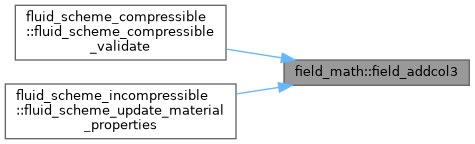
◆ field_addcol3()

subroutine, public field_math::field_addcol3	(	type(field_t), intent(inout)	a,
		type(field_t), intent(in)	b,
		type(field_t), intent(in)	c,
		integer, intent(in), optional	n
	)

Definition at line 594 of file field_math.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ field_addcol4()

subroutine, public field_math::field_addcol4	(	type(field_t), intent(inout)	a,
		type(field_t), intent(in)	b,
		type(field_t), intent(in)	c,
		type(field_t), intent(in)	d,
		integer, intent(in), optional	n
	)

Definition at line 616 of file field_math.f90.

Here is the call graph for this function:

◆ field_addsqr2s2()

subroutine, public field_math::field_addsqr2s2	(	type(field_t), intent(inout)	a,
		type(field_t), intent(in)	b,
		real(kind=rp), intent(in)	c1,
		integer, intent(in), optional	n
	)

Definition at line 440 of file field_math.f90.

Here is the call graph for this function:

◆ field_cadd()

subroutine, public field_math::field_cadd	(	type(field_t), intent(inout)	a,
		real(kind=rp), intent(in)	s,
		integer, intent(in), optional	n
	)

Definition at line 176 of file field_math.f90.

Here is the call graph for this function:

◆ field_cfill()

subroutine, public field_math::field_cfill	(	type(field_t), intent(inout)	a,
		real(kind=rp), intent(in)	c,
		integer, intent(in), optional	n
	)

Definition at line 196 of file field_math.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ field_cmult()

subroutine, public field_math::field_cmult	(	type(field_t), intent(inout)	a,
		real(kind=rp), intent(in)	c,
		integer, intent(in), optional	n
	)

Definition at line 156 of file field_math.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ field_cmult2()

subroutine, public field_math::field_cmult2	(	type(field_t), intent(inout)	a,
		type(field_t), intent(in)	b,
		real(kind=rp), intent(in)	c,
		integer, intent(in), optional	n
	)

Definition at line 462 of file field_math.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ field_col2()

subroutine, public field_math::field_col2	(	type(field_t), intent(inout)	a,
		type(field_t), intent(in)	b,
		integer, intent(in), optional	n
	)

Definition at line 506 of file field_math.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ field_col3()

subroutine, public field_math::field_col3	(	type(field_t), intent(inout)	a,
		type(field_t), intent(in)	b,
		type(field_t), intent(in)	c,
		integer, intent(in), optional	n
	)

Definition at line 527 of file field_math.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ field_copy()

subroutine, public field_math::field_copy	(	type(field_t), intent(inout)	a,
		type(field_t), intent(in)	b,
		integer, intent(in), optional	n
	)

Definition at line 136 of file field_math.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ field_cpwmax2()

subroutine, public field_math::field_cpwmax2	(	type(field_t), intent(inout)	a,
		real(kind=rp), intent(in)	b,
		integer, intent(in), optional	n
	)

Definition at line 814 of file field_math.f90.

Here is the call graph for this function:

◆ field_cpwmax3()

subroutine, public field_math::field_cpwmax3	(	type(field_t), intent(inout)	a,
		type(field_t), intent(in)	b,
		real(kind=rp), intent(in)	c,
		integer, intent(in), optional	n
	)

Definition at line 836 of file field_math.f90.

Here is the call graph for this function:

◆ field_cpwmin2()

subroutine, public field_math::field_cpwmin2	(	type(field_t), intent(inout)	a,
		real(kind=rp), intent(in)	b,
		integer, intent(in), optional	n
	)

Definition at line 903 of file field_math.f90.

Here is the call graph for this function:

◆ field_cpwmin3()

subroutine, public field_math::field_cpwmin3	(	type(field_t), intent(inout)	a,
		type(field_t), intent(in)	b,
		real(kind=rp), intent(in)	c,
		integer, intent(in), optional	n
	)

Definition at line 925 of file field_math.f90.

Here is the call graph for this function:

◆ field_glsc2()

real(kind=rp) function, public field_math::field_glsc2	(	type(field_t), intent(in)	a,
		type(field_t), intent(in)	b,
		integer, intent(in), optional	n
	)

Definition at line 658 of file field_math.f90.

Here is the call graph for this function:

◆ field_glsc3()

real(kind=rp) function, public field_math::field_glsc3	(	type(field_t), intent(in)	a,
		type(field_t), intent(in)	b,
		type(field_t), intent(in)	c,
		integer, intent(in), optional	n
	)

Definition at line 678 of file field_math.f90.

Here is the call graph for this function:

◆ field_glsubnorm()

real(kind=rp) function, public field_math::field_glsubnorm	(	type(field_t), intent(in)	a,
		type(field_t), intent(in)	b,
		integer, intent(in), optional	n
	)

Definition at line 698 of file field_math.f90.

Here is the call graph for this function:

◆ field_glsum()

real(kind=rp) function, public field_math::field_glsum	(	type(field_t), intent(in)	a,
		integer, intent(in), optional	n
	)

Definition at line 638 of file field_math.f90.

Here is the call graph for this function:

◆ field_invcol1()

subroutine, public field_math::field_invcol1	(	type(field_t), intent(inout)	a,
		integer, intent(in), optional	n
	)

Definition at line 216 of file field_math.f90.

Here is the call graph for this function:

◆ field_invcol2()

subroutine, public field_math::field_invcol2	(	type(field_t), intent(inout)	a,
		type(field_t), intent(in)	b,
		integer, intent(in), optional	n
	)

Definition at line 484 of file field_math.f90.

Here is the call graph for this function:

◆ field_invcol3()

subroutine, public field_math::field_invcol3	(	type(field_t), intent(inout)	a,
		type(field_t), intent(in)	b,
		type(field_t), intent(in)	c,
		integer, intent(in), optional	n
	)

Definition at line 236 of file field_math.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

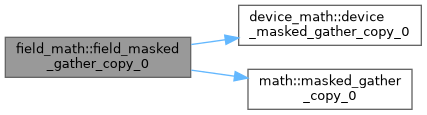
◆ field_masked_gather_copy_0()

subroutine, public field_math::field_masked_gather_copy_0	(	real(kind=rp), dimension(n_mask), intent(inout)	a,
		type(field_t)	b,
		integer, dimension(0:n_mask)	mask,
		integer, intent(in)	n,
		integer, intent(in)	n_mask
	)

Parameters

a	Destination array of size `n_mask`.
b	Source array of size `n`.
mask	Mask array of length n_mask + 1, where `mask(0) = n_mask` the length of the mask array.
n	Size of the field `b`.
n_mask	Size of the mask array `mask` and `a`.

Definition at line 726 of file field_math.f90.

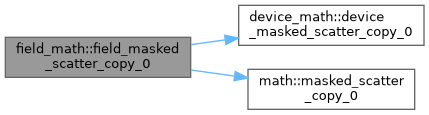
Here is the call graph for this function:

◆ field_masked_scatter_copy_0()

subroutine, public field_math::field_masked_scatter_copy_0	(	type(field_t), intent(inout)	a,
		real(kind=rp), dimension(n_mask), intent(in)	b,
		integer, dimension(0:n_mask)	mask,
		integer, intent(in)	n,
		integer, intent(in)	n_mask
	)

Parameters

a	Destination field.
b	Source array of size `n_mask`.
mask	Mask array of length n_mask + 1, where `mask(0) = n_mask` the length of the mask array.
n	Size of the field `a`.
n_mask	Size of the mask array `mask` and `b`.

Definition at line 751 of file field_math.f90.

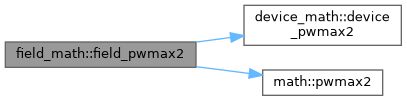
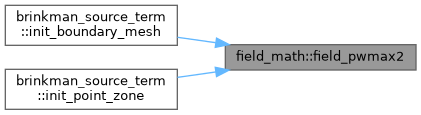
Here is the call graph for this function:

◆ field_pwmax2()

subroutine, public field_math::field_pwmax2	(	type(field_t), intent(inout)	a,
		type(field_t), intent(in)	b,
		integer, intent(in), optional	n
	)

Definition at line 770 of file field_math.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ field_pwmax3()

subroutine, public field_math::field_pwmax3	(	type(field_t), intent(inout)	a,
		type(field_t), intent(in)	b,
		type(field_t), intent(in)	c,
		integer, intent(in), optional	n
	)

Definition at line 792 of file field_math.f90.

Here is the call graph for this function:

◆ field_pwmin2()

subroutine, public field_math::field_pwmin2	(	type(field_t), intent(inout)	a,
		type(field_t), intent(in)	b,
		integer, intent(in), optional	n
	)

Definition at line 859 of file field_math.f90.

Here is the call graph for this function:

◆ field_pwmin3()

subroutine, public field_math::field_pwmin3	(	type(field_t), intent(inout)	a,
		type(field_t), intent(in)	b,
		type(field_t), intent(in)	c,
		integer, intent(in), optional	n
	)

Definition at line 881 of file field_math.f90.

Here is the call graph for this function:

◆ field_rone()

subroutine, public field_math::field_rone	(	type(field_t), intent(inout)	a,
		integer, intent(in), optional	n
	)

Definition at line 117 of file field_math.f90.

Here is the call graph for this function:

◆ field_rzero()

subroutine, public field_math::field_rzero	(	type(field_t), intent(inout)	a,
		integer, intent(in), optional	n
	)

Definition at line 98 of file field_math.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ field_sub2()

subroutine, public field_math::field_sub2	(	type(field_t), intent(inout)	a,
		type(field_t), intent(inout)	b,
		integer, intent(in), optional	n
	)

Definition at line 350 of file field_math.f90.

Here is the call graph for this function:

◆ field_sub3()

subroutine, public field_math::field_sub3	(	type(field_t), intent(inout)	a,
		type(field_t), intent(in)	b,
		type(field_t), intent(in)	c,
		integer, intent(in), optional	n
	)

Definition at line 371 of file field_math.f90.

Here is the call graph for this function:

◆ field_subcol3()

subroutine, public field_math::field_subcol3	(	type(field_t), intent(inout)	a,
		type(field_t), intent(in)	b,
		type(field_t), intent(in)	c,
		integer, intent(in), optional	n
	)

Definition at line 549 of file field_math.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ field_vdot3()

subroutine, public field_math::field_vdot3	(	type(field_t), intent(out)	dot,
		type(field_t), intent(in)	u1,
		type(field_t), intent(in)	u2,
		type(field_t), intent(in)	u3,
		type(field_t), intent(in)	v1,
		type(field_t), intent(in)	v2,
		type(field_t), intent(in)	v3,
		integer, intent(in), optional	n
	)

Definition at line 259 of file field_math.f90.

Here is the call graph for this function:

Functions/Subroutines

Function/Subroutine Documentation

◆ field_add2()

◆ field_add2s1()

◆ field_add2s2()

◆ field_add3()

◆ field_add3s2()

◆ field_add4()

◆ field_addcol3()

◆ field_addcol4()

◆ field_addsqr2s2()

◆ field_cadd()

◆ field_cfill()

◆ field_cmult()

◆ field_cmult2()

◆ field_col2()

◆ field_col3()

◆ field_copy()

◆ field_cpwmax2()

◆ field_cpwmax3()

◆ field_cpwmin2()

◆ field_cpwmin3()

◆ field_glsc2()

◆ field_glsc3()

◆ field_glsubnorm()

◆ field_glsum()

◆ field_invcol1()

◆ field_invcol2()

◆ field_invcol3()

◆ field_masked_gather_copy_0()

◆ field_masked_scatter_copy_0()

◆ field_pwmax2()

◆ field_pwmax3()

◆ field_pwmin2()

◆ field_pwmin3()

◆ field_rone()

◆ field_rzero()

◆ field_sub2()

◆ field_sub3()

◆ field_subcol3()

◆ field_vdot3()