LIBRARY ROUTINES FOR SPECTRAL METHODS. More...

Functions/Subroutines
subroutine	zwgl (z, w, np)
	Generate `NP` Gauss Legendre points `Z` and weights `W` associated with Jacobi polynomial \( P(N)(\alpha=0, \beta=0) \). The polynomial degree `N = NP-1`.

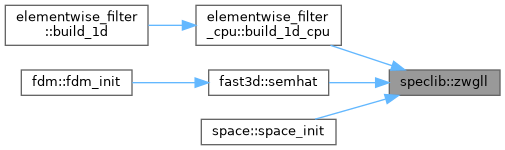
subroutine	zwgll (z, w, np)
	Generate NP Gauss-Lobatto Legendre points (Z) and weights (W) associated with Jacobi polynomial P(N)(alpha=0,beta=0). The polynomial degree N=NP-1. Z and W are in single precision, but all the arithmetic operations are done in double precision.

subroutine	zwgj (z, w, np, alpha, beta)
	Generate NP GAUSS JACOBI points (Z) and weights (W) associated with Jacobi polynomial P(N)(alpha>-1,beta>-1). The polynomial degree N=NP-1. Single precision version.

subroutine	zwgjd (z, w, np, alpha, beta)
	Generate NP GAUSS JACOBI points (Z) and weights (W) associated with Jacobi polynomial P(N)(alpha>-1,beta>-1). The polynomial degree N=NP-1. Double precision version.

subroutine	zwglj (z, w, np, alpha, beta)
	Generate NP GAUSS LOBATTO JACOBI points (Z) and weights (W) associated with Jacobi polynomial P(N)(alpha>-1,beta>-1). The polynomial degree N=NP-1. Single precision version.

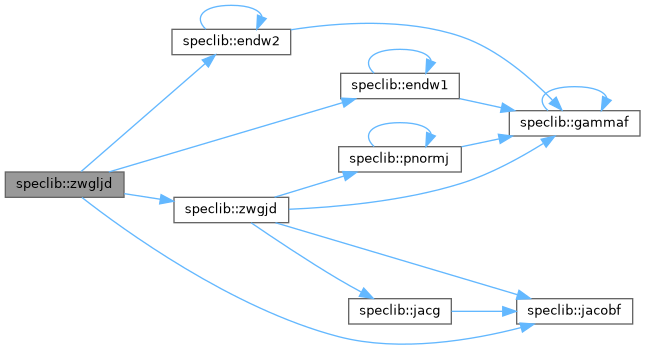
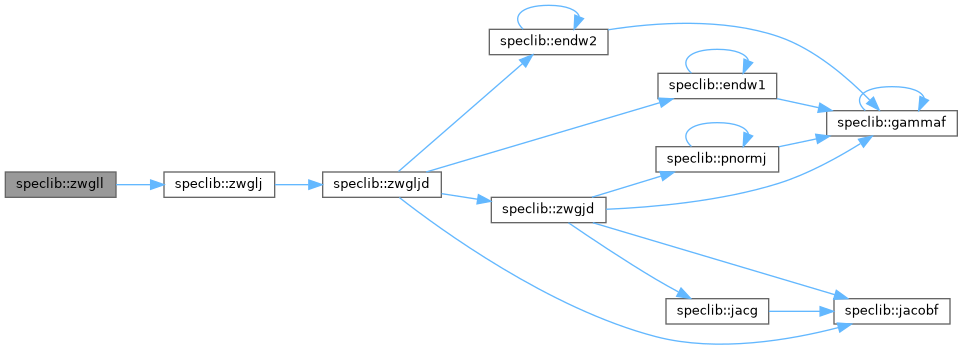
subroutine	zwgljd (z, w, np, alpha, beta)
	Generate NP GAUSS LOBATTO JACOBI points (Z) and weights (W) associated with Jacobi polynomial P(N)(alpha>-1,beta>-1). The polynomial degree N=NP-1. Double precision version.

real(kind=xp) function	endw1 (n, alpha, beta)

real(kind=xp) function	endw2 (n, alpha, beta)

real(kind=xp) function	gammaf (x)

real(kind=xp) function	pnormj (n, alpha, beta)

subroutine	jacg (xjac, np, alpha, beta)
	Compute NP Gauss points XJAC, which are the zeros of the Jacobi polynomial J(NP) with parameters ALPHA and BETA. ALPHA and BETA determines the specific type of Gauss points. Examples: ALPHA = BETA = 0.0 -> Legendre points ALPHA = BETA = -0.5 -> Chebyshev points.

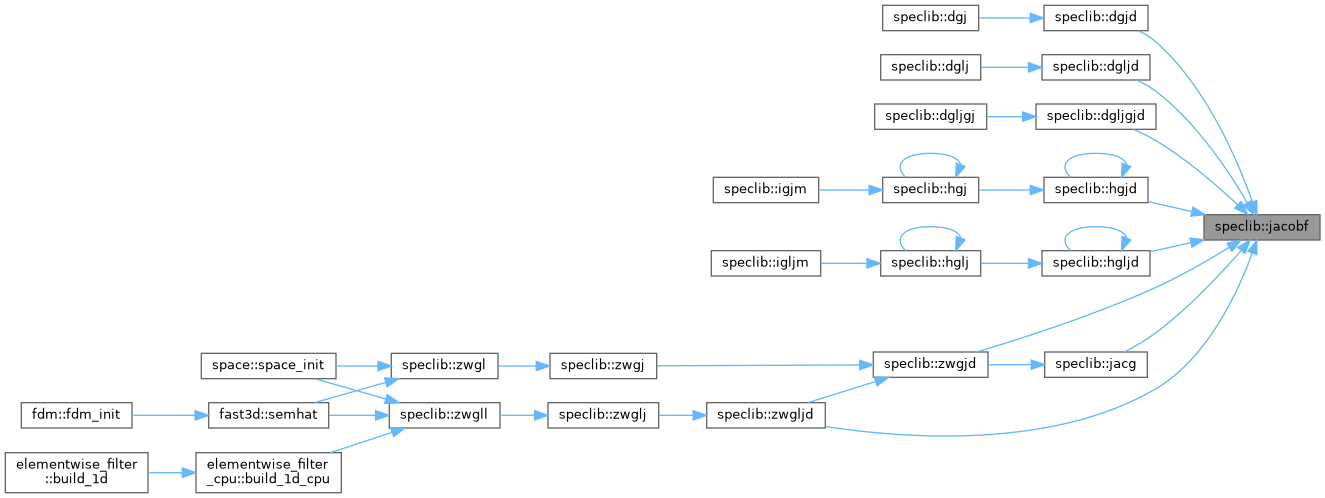
subroutine	jacobf (poly, pder, polym1, pderm1, polym2, pderm2, n, alp, bet, x)
	Computes the Jacobi polynomial (POLY) and its derivative (PDER) of degree N at X.

real(kind=xp) function	hgj (ii, z, zgj, np, alpha, beta)
	Compute the value of the Lagrangian interpolant HGJ through the NP Gauss Jacobi points ZGJ at the point Z. Single precision version.

real(kind=xp) function	hgjd (ii, z, zgj, np, alpha, beta)
	Compute the value of the Lagrangian interpolant HGJD through the NZ Gauss-Lobatto Jacobi points ZGJ at the point Z. Double precision version.

real(kind=xp) function	hglj (ii, z, zglj, np, alpha, beta)
	Compute the value of the Lagrangian interpolant HGLJ through the NZ Gauss-Lobatto Jacobi points ZGLJ at the point Z. Single precision version.

real(kind=xp) function	hgljd (i, z, zglj, np, alpha, beta)
	Compute the value of the Lagrangian interpolant HGLJD through the NZ Gauss-Lobatto Jacobi points ZJACL at the point Z. Double precision version.

subroutine	dgj (d, dt, z, nz, nzd, alpha, beta)
	Compute the derivative matrix D and its transpose DT associated with the Nth order Lagrangian interpolants through the NZ Gauss Jacobi points Z. Note: D and DT are square matrices. Single precision version.

subroutine	dgjd (d, dt, z, nz, nzd, alpha, beta)
	Compute the derivative matrix D and its transpose DT associated with the Nth order Lagrangian interpolants through the NZ Gauss Jacobi points Z. Note: D and DT are square matrices. Double precision version.

subroutine	dglj (d, dt, z, nz, nzd, alpha, beta)
	Compute the derivative matrix D and its transpose DT associated with the Nth order Lagrangian interpolants through the NZ Gauss-Lobatto Jacobi points Z. Note: D and DT are square matrices. Single precision version.

subroutine	dgljd (d, dt, z, nz, nzd, alpha, beta)
	Compute the derivative matrix D and its transpose DT associated with the Nth order Lagrangian interpolants through the NZ Gauss-Lobatto Jacobi points Z. Note: D and DT are square matrices. Double precision version.

subroutine	dgll (d, dt, z, nz, nzd)
	Compute the derivative matrix D and its transpose DT associated with the Nth order Lagrangian interpolants through the NZ Gauss-Lobatto Legendre points Z. Note: D and DT are square matrices.

real(kind=xp) function	hgll (i, z, zgll, nz)
	Compute the value of the Lagrangian interpolant L through the NZ Gauss-Lobatto Legendre points ZGLL at the point Z.

real(kind=xp) function	hgl (i, z, zgl, nz)
	Compute the value of the Lagrangian interpolant HGL through the NZ Gauss Legendre points ZGL at the point Z.

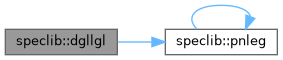
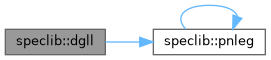
real(kind=xp) function	pnleg (z, n)
	Compute the value of the Nth order Legendre polynomial at Z. (Simpler than JACOBF) Based on the recursion formula for the Legendre polynomials.

subroutine	legendre_poly (l, x, n)
	Evaluate Legendre polynomials of degrees 0-N at point x and store in array L.

real(kind=xp) function	pndleg (z, n)
	Compute the derivative of the Nth order Legendre polynomial at Z. (Simpler than JACOBF) Based on the recursion formula for the Legendre polynomials.

subroutine	dgllgl (d, dt, zm1, zm2, im12, nzm1, nzm2, nd1, nd2)
	Compute the (one-dimensional) derivative matrix D and its transpose DT associated with taking the derivative of a variable expanded on a Gauss-Lobatto Legendre mesh (M1), and evaluate its derivative on a Guass Legendre mesh (M2). Need the one-dimensional interpolation operator IM12 (see subroutine IGLLGL). Note: D and DT are rectangular matrices.

subroutine	dgljgj (d, dt, zgl, zg, iglg, npgl, npg, nd1, nd2, alpha, beta)
	Compute the (one-dimensional) derivative matrix D and its transpose DT associated with taking the derivative of a variable expanded on a Gauss-Lobatto Jacobi mesh (M1), and evaluate its derivative on a Guass Jacobi mesh (M2). Need the one-dimensional interpolation operator IM12 (see subroutine IGLJGJ). Note: D and DT are rectangular matrices. Single precision version.

subroutine	dgljgjd (d, dt, zgl, zg, iglg, npgl, npg, nd1, nd2, alpha, beta)
	Compute the (one-dimensional) derivative matrix D and its transpose DT associated with taking the derivative of a variable expanded on a Gauss-Lobatto Jacobi mesh (M1), and evaluate its derivative on a Guass Jacobi mesh (M2). Need the one-dimensional interpolation operator IM12 (see subroutine IGLJGJ). Note: D and DT are rectangular matrices. Double precision version.

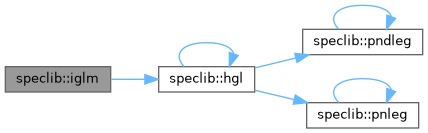
subroutine	iglm (i12, it12, z1, z2, nz1, nz2, nd1, nd2)
	Compute the one-dimensional interpolation operator (matrix) I12 ands its transpose IT12 for interpolating a variable from a Gauss Legendre mesh (1) to a another mesh M (2). Z1 : NZ1 Gauss Legendre points. Z2 : NZ2 points on mesh M.

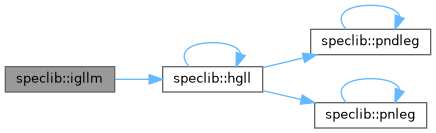
subroutine	igllm (i12, it12, z1, z2, nz1, nz2, nd1, nd2)
	Compute the one-dimensional interpolation operator (matrix) I12 ands its transpose IT12 for interpolating a variable from a Gauss-Lobatto Legendre mesh (1) to a another mesh M (2). Z1 : NZ1 Gauss-Lobatto Legendre points. Z2 : NZ2 points on mesh M.

subroutine	igjm (i12, it12, z1, z2, nz1, nz2, nd1, nd2, alpha, beta)
	Compute the one-dimensional interpolation operator (matrix) I12 ands its transpose IT12 for interpolating a variable from a Gauss Jacobi mesh (1) to a another mesh M (2). Z1 : NZ1 Gauss Jacobi points. Z2 : NZ2 points on mesh M. Single precision version.

subroutine	igljm (i12, it12, z1, z2, nz1, nz2, nd1, nd2, alpha, beta)
	Compute the one-dimensional interpolation operator (matrix) I12 ands its transpose IT12 for interpolating a variable from a Gauss-Lobatto Jacobi mesh (1) to a another mesh M (2). Z1 : NZ1 Gauss-Lobatto Jacobi points. Z2 : NZ2 points on mesh M. Single precision version.

Detailed Description

March 1989

For questions, comments or suggestions, please contact:

Einar Malvin Ronquist Room 3-243 Department of Mechanical Engineering Massachusetts Institute of Technology 77 Massachusetts Avenue Cambridge, MA 0299 U.S.A.

Function/Subroutine Documentation

◆ dgj()

subroutine speclib::dgj	(	real(kind=xp), dimension(nzd, nzd), intent(inout)	d,
		real(kind=xp), dimension(nzd, nzd), intent(inout)	dt,
		real(kind=xp), dimension(nz), intent(in)	z,
		integer, intent(in)	nz,
		integer, intent(in)	nzd,
		real(kind=xp), intent(in)	alpha,
		real(kind=xp), intent(in)	beta
	)

Definition at line 714 of file speclib.f90.

Here is the call graph for this function:

◆ dgjd()

subroutine speclib::dgjd	(	real(kind=xp), dimension(nzd, nzd), intent(inout)	d,
		real(kind=xp), dimension(nzd, nzd), intent(inout)	dt,
		real(kind=xp), dimension(nz), intent(in)	z,
		integer, intent(in)	nz,
		integer, intent(in)	nzd,
		real(kind=xp), intent(in)	alpha,
		real(kind=xp), intent(in)	beta
	)

Definition at line 753 of file speclib.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ dglj()

subroutine speclib::dglj	(	real(kind=xp), dimension(nzd, nzd), intent(inout)	d,
		real(kind=xp), dimension(nzd, nzd), intent(inout)	dt,
		real(kind=xp), dimension(nz), intent(in)	z,
		integer, intent(in)	nz,
		integer, intent(in)	nzd,
		real(kind=xp), intent(in)	alpha,
		real(kind=xp), intent(in)	beta
	)

Definition at line 792 of file speclib.f90.

Here is the call graph for this function:

◆ dgljd()

subroutine speclib::dgljd	(	real(kind=xp), dimension(nzd, nzd), intent(inout)	d,
		real(kind=xp), dimension(nzd, nzd), intent(inout)	dt,
		real(kind=xp), dimension(nz), intent(in)	z,
		integer, intent(in)	nz,
		integer, intent(in)	nzd,
		real(kind=xp), intent(in)	alpha,
		real(kind=xp), intent(in)	beta
	)

Definition at line 831 of file speclib.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ dgljgj()

subroutine speclib::dgljgj	(	real(kind=xp), dimension(nd2, nd1), intent(inout)	d,
		real(kind=xp), dimension(nd1, nd2), intent(inout)	dt,
		real(kind=xp), dimension(nd1), intent(in)	zgl,
		real(kind=xp), dimension(nd2), intent(in)	zg,
		real(kind=xp), dimension(nd2, nd1), intent(in)	iglg,
		integer, intent(in)	npgl,
		integer, intent(in)	npg,
		integer, intent(in)	nd1,
		integer, intent(in)	nd2,
		real(kind=xp), intent(in)	alpha,
		real(kind=xp), intent(in)	beta
	)

Definition at line 1095 of file speclib.f90.

Here is the call graph for this function:

◆ dgljgjd()

subroutine speclib::dgljgjd	(	real(kind=xp), dimension(nd2, nd1), intent(inout)	d,
		real(kind=xp), dimension(nd1, nd2), intent(inout)	dt,
		real(kind=xp), dimension(nd1), intent(in)	zgl,
		real(kind=xp), dimension(nd2), intent(in)	zg,
		real(kind=xp), dimension(nd2, nd1), intent(in)	iglg,
		integer, intent(in)	npgl,
		integer, intent(in)	npg,
		integer, intent(in)	nd1,
		integer, intent(in)	nd2,
		real(kind=xp), intent(in)	alpha,
		real(kind=xp), intent(in)	beta
	)

Definition at line 1144 of file speclib.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ dgll()

subroutine speclib::dgll	(	real(kind=rp), dimension(nzd, nzd), intent(inout)	d,
		real(kind=rp), dimension(nzd, nzd), intent(inout)	dt,
		real(kind=rp), dimension(nz), intent(in)	z,
		integer, intent(in)	nz,
		integer, intent(in)	nzd
	)

Definition at line 879 of file speclib.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ dgllgl()

subroutine speclib::dgllgl	(	real(kind=xp), dimension(nd2, nd1), intent(inout)	d,
		real(kind=xp), dimension(nd1, nd2), intent(inout)	dt,
		real(kind=xp), dimension(nd1), intent(in)	zm1,
		real(kind=xp), dimension(nd2), intent(in)	zm2,
		real(kind=xp), dimension(nd2, nd1), intent(in)	im12,
		integer, intent(in)	nzm1,
		integer, intent(in)	nzm2,
		integer, intent(in)	nd1,
		integer, intent(in)	nd2
	)

Definition at line 1057 of file speclib.f90.

Here is the call graph for this function:

◆ endw1()

real(kind=xp) function speclib::endw1	(	integer, intent(in)	n,
		real(kind=xp), intent(in)	alpha,
		real(kind=xp), intent(in)	beta
	)

Todo:: document ENDW1

Definition at line 346 of file speclib.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ endw2()

real(kind=xp) function speclib::endw2	(	integer, intent(in)	n,
		real(kind=xp), intent(in)	alpha,
		real(kind=xp), intent(in)	beta
	)

Todo:: document ENDW2

Definition at line 395 of file speclib.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ gammaf()

real(kind=xp) function speclib::gammaf ( real(kind=xp), intent(in) x )

Todo:: document GAMMAF

Definition at line 445 of file speclib.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ hgj()

real(kind=xp) function speclib::hgj	(	integer, intent(in)	ii,
		real(kind=xp), intent(in)	z,
		real(kind=xp), dimension(np), intent(in)	zgj,
		integer, intent(in)	np,
		real(kind=xp), intent(in)	alpha,
		real(kind=xp), intent(in)	beta
	)

Definition at line 606 of file speclib.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ hgjd()

real(kind=xp) function speclib::hgjd	(	integer, intent(in)	ii,
		real(kind=xp), intent(in)	z,
		real(kind=xp), dimension(np), intent(in)	zgj,
		integer, intent(in)	np,
		real(kind=xp), intent(in)	alpha,
		real(kind=xp), intent(in)	beta
	)

Definition at line 634 of file speclib.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ hgl()

real(kind=xp) function speclib::hgl	(	integer, intent(in)	i,
		real(kind=xp), intent(in)	z,
		real(kind=xp), dimension(nz), intent(in)	zgl,
		integer, intent(in)	nz
	)

Definition at line 945 of file speclib.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ hglj()

real(kind=xp) function speclib::hglj	(	integer, intent(in)	ii,
		real(kind=xp), intent(in)	z,
		real(kind=xp), dimension(np), intent(in)	zglj,
		integer, intent(in)	np,
		real(kind=xp), intent(in)	alpha,
		real(kind=xp), intent(in)	beta
	)

Definition at line 656 of file speclib.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ hgljd()

real(kind=xp) function speclib::hgljd	(	integer, intent(in)	i,
		real(kind=xp), intent(in)	z,
		real(kind=xp), dimension(np), intent(in)	zglj,
		integer, intent(in)	np,
		real(kind=xp), intent(in)	alpha,
		real(kind=xp), intent(in)	beta
	)

Definition at line 683 of file speclib.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ hgll()

real(kind=xp) function speclib::hgll	(	integer, intent(in)	i,
		real(kind=xp), intent(in)	z,
		real(kind=xp), dimension(nz), intent(in)	zgll,
		integer, intent(in)	nz
	)

Definition at line 922 of file speclib.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ igjm()

subroutine speclib::igjm	(	real(kind=xp), dimension(nd2, nd1), intent(inout)	i12,
		real(kind=xp), dimension(nd1, nd2), intent(inout)	it12,
		real(kind=xp), dimension(nd1), intent(in)	z1,
		real(kind=xp), dimension(nd2), intent(in)	z2,
		integer, intent(in)	nz1,
		integer, intent(in)	nz2,
		integer, intent(in)	nd1,
		integer, intent(in)	nd2,
		real(kind=xp), intent(in)	alpha,
		real(kind=xp), intent(in)	beta
	)

Definition at line 1246 of file speclib.f90.

Here is the call graph for this function:

◆ igljm()

subroutine speclib::igljm	(	real(kind=xp), dimension(nd2, nd1), intent(inout)	i12,
		real(kind=xp), dimension(nd1, nd2), intent(inout)	it12,
		real(kind=xp), dimension(nd1), intent(in)	z1,
		real(kind=xp), dimension(nd2), intent(in)	z2,
		integer, intent(in)	nz1,
		integer, intent(in)	nz2,
		integer, intent(in)	nd1,
		integer, intent(in)	nd2,
		real(kind=xp), intent(in)	alpha,
		real(kind=xp), intent(in)	beta
	)

Definition at line 1274 of file speclib.f90.

Here is the call graph for this function:

◆ igllm()

subroutine speclib::igllm	(	real(kind=xp), dimension(nd2, nd1), intent(inout)	i12,
		real(kind=xp), dimension(nd1, nd2), intent(inout)	it12,
		real(kind=xp), dimension(nd1), intent(in)	z1,
		real(kind=xp), dimension(nd2), intent(in)	z2,
		integer, intent(in)	nz1,
		integer, intent(in)	nz2,
		integer, intent(in)	nd1,
		integer, intent(in)	nd2
	)

Definition at line 1218 of file speclib.f90.

Here is the call graph for this function:

◆ iglm()

subroutine speclib::iglm	(	real(kind=xp), dimension(nd2, nd1), intent(inout)	i12,
		real(kind=xp), dimension(nd1, nd2), intent(inout)	it12,
		real(kind=xp), dimension(nd1), intent(in)	z1,
		real(kind=xp), dimension(nd2), intent(in)	z2,
		integer, intent(in)	nz1,
		integer, intent(in)	nz2,
		integer, intent(in)	nd1,
		integer, intent(in)	nd2
	)

Definition at line 1191 of file speclib.f90.

Here is the call graph for this function:

◆ jacg()

subroutine speclib::jacg	(	real(kind=xp), dimension(np), intent(inout)	xjac,
		integer, intent(in)	np,
		real(kind=xp), intent(in)	alpha,
		real(kind=xp), intent(in)	beta
	)

Definition at line 499 of file speclib.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ jacobf()

subroutine speclib::jacobf	(	real(kind=xp), intent(inout)	poly,
		real(kind=xp), intent(inout)	pder,
		real(kind=xp), intent(inout)	polym1,
		real(kind=xp), intent(inout)	pderm1,
		real(kind=xp), intent(inout)	polym2,
		real(kind=xp), intent(inout)	pderm2,
		integer, intent(in)	n,
		real(kind=xp), intent(in)	alp,
		real(kind=xp), intent(in)	bet,
		real(kind=xp), intent(in)	x
	)

Definition at line 558 of file speclib.f90.

Here is the caller graph for this function:

◆ legendre_poly()

subroutine speclib::legendre_poly	(	real(kind=rp), dimension(0:n), intent(inout)	l,
		real(kind=rp), intent(in)	x,
		integer, intent(in)	n
	)

Definition at line 999 of file speclib.f90.

Here is the caller graph for this function:

◆ pndleg()

real(kind=xp) function speclib::pndleg	(	real(kind=xp), intent(in)	z,
		integer, intent(in)	n
	)

Definition at line 1020 of file speclib.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

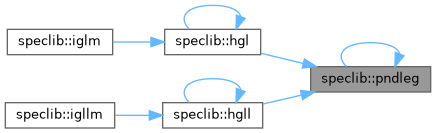
◆ pnleg()

real(kind=xp) function speclib::pnleg	(	real(kind=xp), intent(in)	z,
		integer, intent(in)	n
	)

Definition at line 966 of file speclib.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

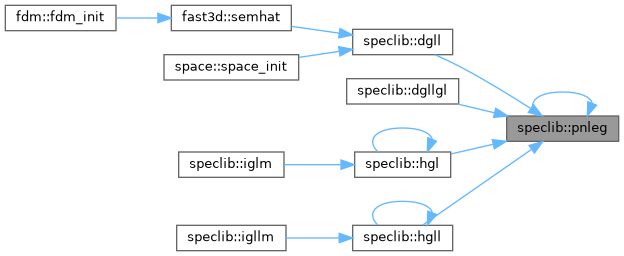
◆ pnormj()

real(kind=xp) function speclib::pnormj	(	integer, intent(in)	n,
		real(kind=xp), intent(in)	alpha,
		real(kind=xp), intent(in)	beta
	)

Todo:: document PNORMJ

Definition at line 464 of file speclib.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ zwgj()

subroutine speclib::zwgj	(	real(kind=rp), dimension(np), intent(inout)	z,
		real(kind=rp), dimension(np), intent(inout)	w,
		integer, intent(in)	np,
		real(kind=rp), intent(in)	alpha,
		real(kind=rp), intent(in)	beta
	)

Definition at line 191 of file speclib.f90.

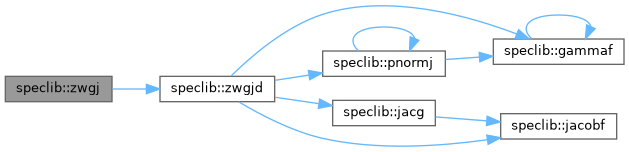
Here is the call graph for this function:

Here is the caller graph for this function:

◆ zwgjd()

subroutine speclib::zwgjd	(	real(kind=xp), dimension(np), intent(inout)	z,
		real(kind=xp), dimension(np), intent(inout)	w,
		integer, intent(in)	np,
		real(kind=xp), intent(in)	alpha,
		real(kind=xp), intent(in)	beta
	)

Definition at line 223 of file speclib.f90.

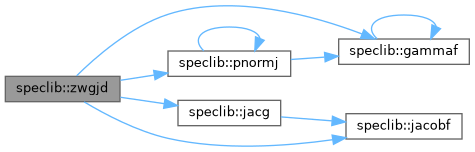
Here is the call graph for this function:

Here is the caller graph for this function:

◆ zwgl()

subroutine speclib::zwgl	(	real(kind=rp), dimension(np), intent(inout)	z,
		real(kind=rp), dimension(np), intent(inout)	w,
		integer, intent(in)	np
	)

Parameters

Z	Quadrature points.
W	Quadrature weights.
NP	Number of quadrature points.

Definition at line 163 of file speclib.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ zwglj()

subroutine speclib::zwglj	(	real(kind=rp), dimension(np), intent(inout)	z,
		real(kind=rp), dimension(np), intent(inout)	w,
		integer, intent(in)	np,
		real(kind=rp), intent(in)	alpha,
		real(kind=rp), intent(in)	beta
	)

Definition at line 274 of file speclib.f90.

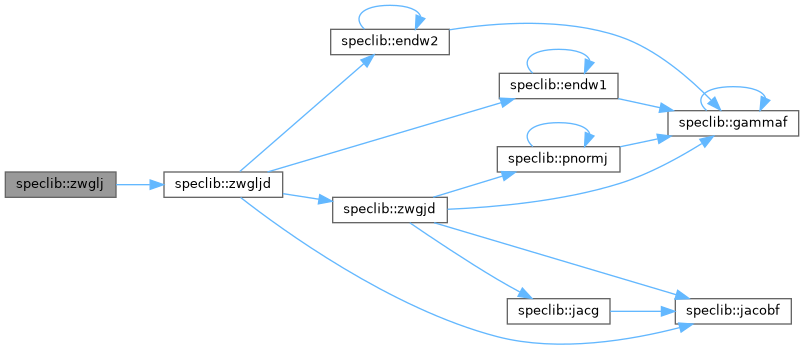
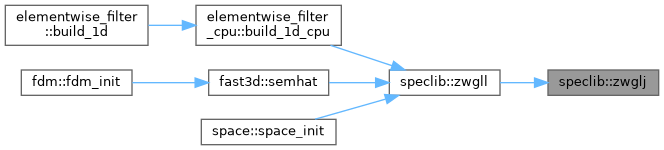
Here is the call graph for this function:

Here is the caller graph for this function:

◆ zwgljd()

subroutine speclib::zwgljd	(	real(kind=xp), dimension(np), intent(inout)	z,
		real(kind=xp), dimension(np), intent(inout)	w,
		integer, intent(in)	np,
		real(kind=xp), intent(in)	alpha,
		real(kind=xp), intent(in)	beta
	)

Definition at line 306 of file speclib.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ zwgll()

subroutine speclib::zwgll	(	real(kind=rp), dimension(np), intent(inout)	z,
		real(kind=rp), dimension(np), intent(inout)	w,
		integer, intent(in)	np
	)

Definition at line 178 of file speclib.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

Functions/Subroutines

Detailed Description

Function/Subroutine Documentation

◆ dgj()

◆ dgjd()

◆ dglj()

◆ dgljd()

◆ dgljgj()

◆ dgljgjd()

◆ dgll()

◆ dgllgl()

◆ endw1()

◆ endw2()

◆ gammaf()

◆ hgj()

◆ hgjd()

◆ hgl()

◆ hglj()

◆ hgljd()

◆ hgll()

◆ igjm()

◆ igljm()

◆ igllm()

◆ iglm()

◆ jacg()

◆ jacobf()

◆ legendre_poly()

◆ pndleg()

◆ pnleg()

◆ pnormj()

◆ zwgj()

◆ zwgjd()

◆ zwgl()

◆ zwglj()

◆ zwgljd()

◆ zwgll()