Routines to obtain interpolated values on a set of points with known rst coordinates in elements local to this process.
|
| type | local_interpolator_t |
| | Interpolation on a set of points with known rst coordinates in elements local to this process. Similar to point_interpolator, but prioritizes performance Only works with arrays of coordinates Performs interpolation with the configured NEKO_BCKND. More...
|
| |
|
| subroutine | local_interpolator_init_3arrays (this, xh, r, s, t, n_points) |
| | Initialization of point interpolation.
|
| |
| subroutine | local_interpolator_init_1array (this, xh, rst, n_points) |
| | Initialization of point interpolation.
|
| |
| subroutine | local_interpolator_free (this) |
| | Free pointers.
|
| |
| subroutine | local_interpolator_compute_weights (this, r, s, t) |
| | Computes interpolation weights \( w_r, w_s, w_t \) for a list of points.
|
| |
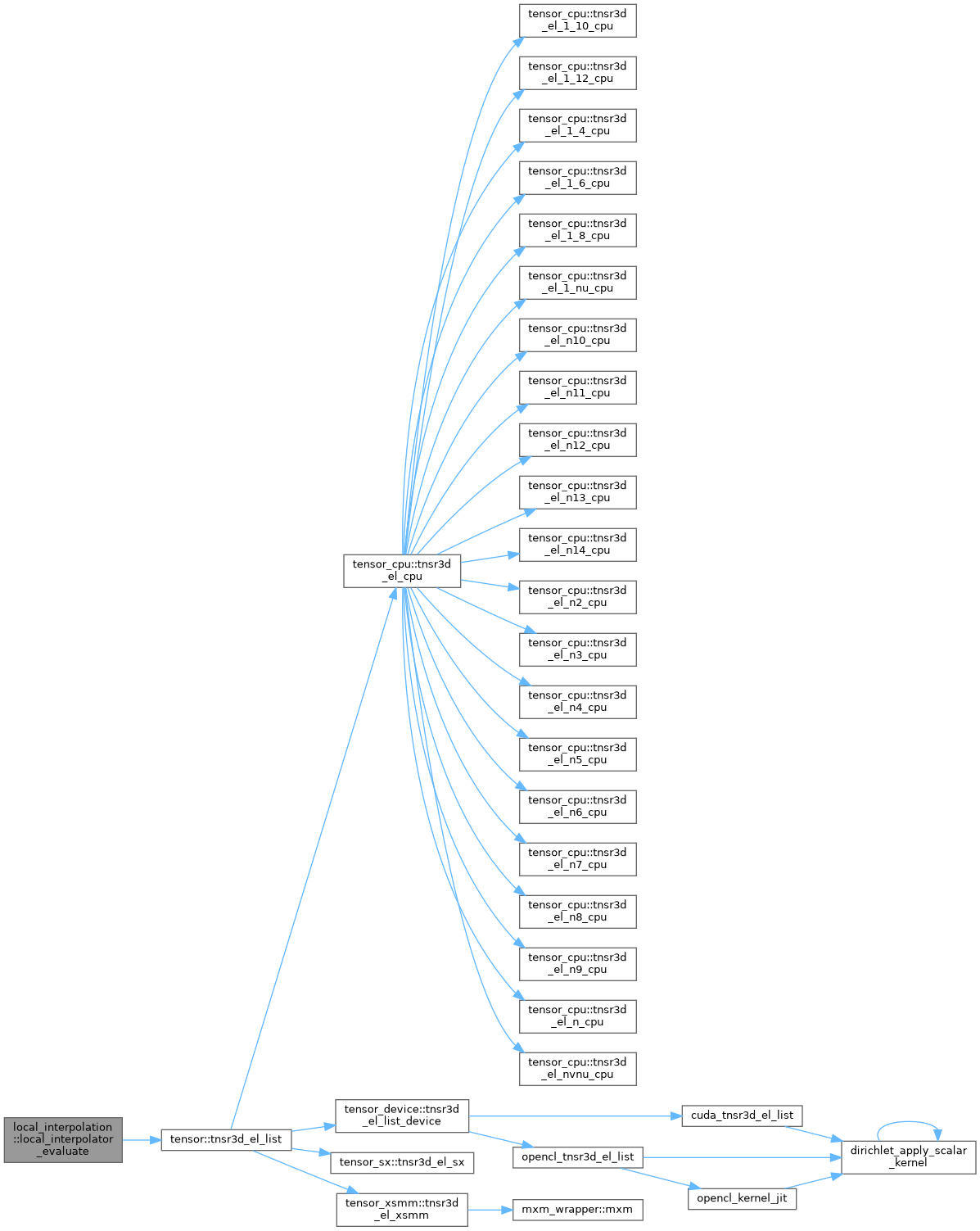
| subroutine | local_interpolator_evaluate (this, interp_values, el_list, field, nel, on_host) |
| | Interpolates a list of fields based on a set of element ids.
|
| |
| subroutine | jacobian (jac, rst, x, y, z, n_pts, xh) |
| | Constructs the Jacobian, returns a 3-by-3 times number of points where \( [J(\mathbf{r}]_{ij} = \frac{d\mathbf{x}_i}{d\mathbf{r}_j}\).
|
| |
| subroutine | jacobian_inverse (jacinv, rst, x, y, z, n_pts, xh) |
| |
◆ jacobian()
| subroutine local_interpolation::jacobian |
( |
real(kind=rp), dimension(3,3, n_pts), intent(out) |
jac, |
|
|
real(kind=rp), dimension(3, n_pts), intent(inout) |
rst, |
|
|
real(kind=rp), dimension(xh%lx, xh%ly, xh%lz, n_pts), intent(inout) |
x, |
|
|
real(kind=rp), dimension(xh%lx, xh%ly, xh%lz, n_pts), intent(inout) |
y, |
|
|
real(kind=rp), dimension(xh%lx, xh%ly, xh%lz, n_pts), intent(inout) |
z, |
|
|
integer, intent(in) |
n_pts, |
|
|
type(space_t), intent(inout) |
xh |
|
) |
| |
|
private |
- Parameters
-
| rst | r,s,t coordinates. |
| X | Values of the field \( X \) at points. |
| Y | Values of the field \( Y \) at points. |
| Z | Values of the field \( Z \) at points. |
Definition at line 242 of file local_interpolation.f90.
◆ jacobian_inverse()
| subroutine local_interpolation::jacobian_inverse |
( |
real(kind=rp), dimension(3,3, n_pts), intent(out) |
jacinv, |
|
|
real(kind=rp), dimension(3, n_pts), intent(inout) |
rst, |
|
|
real(kind=rp), dimension(xh%lx, xh%ly, xh%lz, n_pts), intent(inout) |
x, |
|
|
real(kind=rp), dimension(xh%lx, xh%ly, xh%lz, n_pts), intent(inout) |
y, |
|
|
real(kind=rp), dimension(xh%lx, xh%ly, xh%lz, n_pts), intent(inout) |
z, |
|
|
integer |
n_pts, |
|
|
type(space_t), intent(inout) |
xh |
|
) |
| |
|
private |
◆ local_interpolator_compute_weights()
| subroutine local_interpolation::local_interpolator_compute_weights |
( |
class(local_interpolator_t), intent(inout) |
this, |
|
|
real(kind=rp), dimension(:), intent(in) |
r, |
|
|
real(kind=rp), dimension(:), intent(in) |
s, |
|
|
real(kind=rp), dimension(:), intent(in) |
t |
|
) |
| |
|
private |
- Parameters
-
| r | local r-coordinates. |
| s | local s-coordinates. |
| t | local t-coordinates. |
| wr | Weights in the r-direction. |
| ws | Weights in the s-direction. |
| wt | Weights in the t-direction. |
- Note
wr, ws and wt must be arrays of dimensions (lx, N) where N is the number of points (size of the r,s,t arrays).
Definition at line 184 of file local_interpolation.f90.
◆ local_interpolator_evaluate()
| subroutine local_interpolation::local_interpolator_evaluate |
( |
class(local_interpolator_t), intent(inout) |
this, |
|
|
real(kind=rp), dimension(this%n_points), intent(inout) |
interp_values, |
|
|
integer, dimension(this%n_points), intent(in) |
el_list, |
|
|
real(kind=rp), dimension(this%xh%lxyz, nel), intent(inout) |
field, |
|
|
integer, intent(in) |
nel, |
|
|
logical, intent(in) |
on_host |
|
) |
| |
|
private |
- Parameters
-
| rst | r,s,t coordinates. |
| el_owners | Array of element ids that "own" a given point i. |
| sampled_fields_list | A list of fields to interpolate. |
| wr | Weights in the r-direction of shape (lx, N) where N is the number of points to interpolate. |
| ws | Weights in the s-direction of shape (lx, N) where N is the number of points to interpolate. |
| wt | Weights in the t-direction of shape (lx, N) where N is the number of points to interpolate. |
- Note
- The weights can be generated with the subroutine
compute_weights. Assumes weights have been computed for these points.
Definition at line 221 of file local_interpolation.f90.
◆ local_interpolator_free()
◆ local_interpolator_init_1array()
| subroutine local_interpolation::local_interpolator_init_1array |
( |
class(local_interpolator_t), intent(inout), target |
this, |
|
|
type(space_t), intent(in), target |
xh, |
|
|
real(kind=rp), dimension(3,n_points), intent(in) |
rst, |
|
|
integer, intent(in) |
n_points |
|
) |
| |
|
private |
◆ local_interpolator_init_3arrays()
| subroutine local_interpolation::local_interpolator_init_3arrays |
( |
class(local_interpolator_t), intent(inout), target |
this, |
|
|
type(space_t), intent(in), target |
xh, |
|
|
real(kind=rp), dimension(n_points) |
r, |
|
|
real(kind=rp), dimension(n_points) |
s, |
|
|
real(kind=rp), dimension(n_points) |
t, |
|
|
integer, intent(in) |
n_points |
|
) |
| |